Subsequently, a selection of research papers are listed where GTPack was applied. If you would like to have your paper added to the list, please get in touch with us.
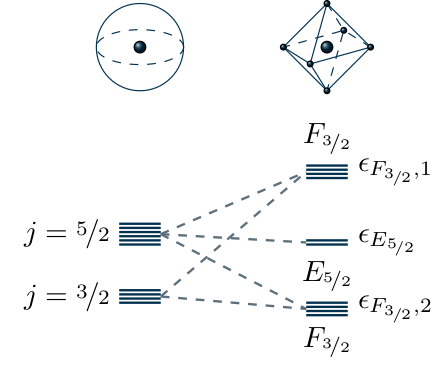
Coordination chemistry in molecular symmetry adapted spin space (mSASS)
R. Matthias Geilhufe and Jeffrey D. Rinehart, arXiv:220903123 (2022)
Many areas of chemistry are devoted to the challenge of understanding, predicting, and controlling the behavior of strongly localized electrons. Examples include molecular magnetism and luminescence, color centers in crystals, photochemistry and quantum sensing to name but a few. Over the years, an amalgam of powerful quantum chemistry methods, simple intuitive models, and phenomenological parameterizations have been developed, providing increasingly complex and specialized methodologies. Even with increasing specialization, a pervasive challenge remains that is surprisingly universal – the simultaneous description of continuous symmetries (e.g. spin and orbital angular momenta) and discrete symmetries (e.g. crystal field). Modeling behavior in these complex systems is increasingly important for metal ions of unusual or technologically relevant behavior. Additionally, development of broad-scope models with physically-meaningful parameters carries the potential to facilitate interdisciplinary collaboration and large-scale meta analysis. We propose a generalized algorithmic approach, the molecular symmetry adapted spin space (mSASS), to localized electronic structure. We derive the Hamiltonian in symmetry-constrained matrix form with an exact account of free parameters and examples. Although preliminary in its implementation, a fundamental benefit of this approach is the treatment of spatial and spin-orbit symmetries without the need for perturbative approximations. In general, the mSASS Hamiltonian is large but finite and can be diagonalized numerically with high efficiency, providing a basis for conceptual models of electronic structure that naturally incorporates spin while leveraging the intuition and efficiency benefits of crystallographic symmetry. For the generation of the mSASS Hamiltonian, we provide an implementation into the Mathematica Software Package, GTPack.
Electron magnetic moment of chiral phonons
R. Matthias Geilhufe and W. Hergert, arXiv:2208.05746 (2022)
High intensity THz lasers allow for the coherent excitation of individual phonon modes. The ultrafast control of emergent magnetism by means of phonons opens up new tuning mechanisms for functional materials. While theoretically predicted phonon magnetic moments are tiny, recent experiments hint towards a significant magnetization in various materials. To explain these phenomena, we derive a coupling mechanism between the phonon angular momentum and the electron spin. This coupling introduces the transient level-splitting of spin-up and spin-down channels and a resulting magnetization. We estimate this magnetization on the example of the lowest infrared active mode in the perovskite KTaO3. Our results show an electronic magnetic moment of ≈0.2 μB per unit cell, depending on the doping level and electron temperature.
Energy density as a probe of band representations in photonic crystals
Topological quantum chemistry (TQC) has recently emerged as an instrumental tool to characterize the topological nature of both fermionic and bosonic band structures. TQC is based on the study of band representations and the localization of maximally localized Wannier functions. In this article, we study various two-dimensional photonic crystal structures analyzing their topological character through a combined study of TQC, their Wilson-loop (WL) spectra and the electromagnetic energy density. Our study demonstrates that the analysis of the spatial localization of the energy density complements the study of the topological properties in terms of the spectrum of the WL operator and TQC.
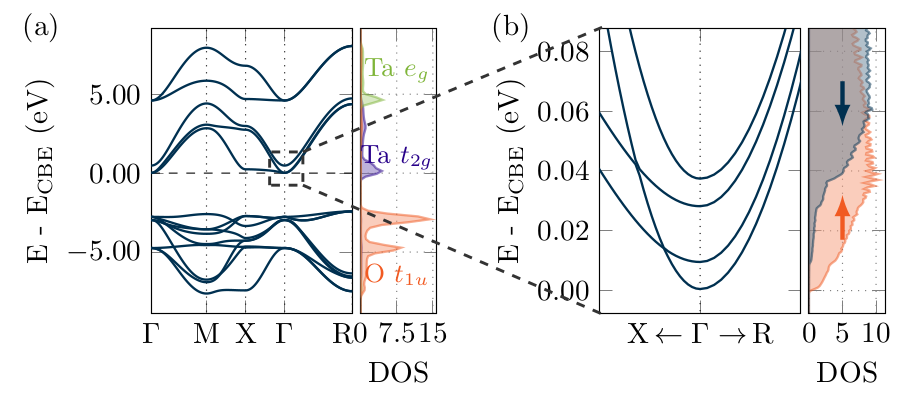
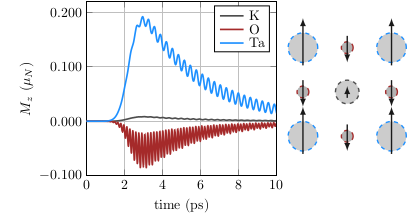
Dynamically induced magnetism in KTaO3
R. Matthias Geilhufe, Vladimir Juričić, Stefano Bonetti, Jian-Xin Zhu, Alexander V. Balatsky, Phys. Rev. Research, 3, L022011 (2021)
Dynamical multiferroicity features entangled dynamic orders: fluctuating electric dipoles induce magnetization. Hence, the material with paraelectric fluctuations can develop magnetic signatures if dynamically driven. We identify the paraelectric KTaO3 (KTO) as a prime candidate for the observation of the dynamical multiferroicity. We show that when a KTO sample is exposed to a circularly polarized laser pulse, the dynamically induced ionic magnetic moments are of the order of 5 % of the nuclear magneton per unit cell. We determine the phonon spectrum using ab initio methods and identify T1u as relevant soft phonon modes that couple to the external field and induce magnetic polarization. We also predict a corresponding electron effect for the dynamically induced magnetic moment which is enhanced by several orders of magnitude due to the significant mass difference between electron and ionic nucleus.
Direct driving of electronic and phononic degrees of freedom in a honeycomb bilayer with infrared light
Martin Rodriguez-Vega, Michael Vogl, Gregory A. Fiete, Phys. Rev. B, 104, 245135 (2021)
We study theoretically AB-stacked honeycomb bilayers driven by light in resonance with an infrared phonon within a tight-binding description. We characterize the phonon properties of honeycomb bilayers with group theory and construct an electronic time-dependent tight-binding model for the system following photoexcitation in resonance with an infrared phonon. We adopt an atomically adiabatic approximation [V. Mohanty and E. J. Heller, Proc. Natl. Acad. Sci. 116, 18316 (2019)] to describe classically vibrating nuclei, but obtain the Floquet quasienergy spectrum associated with the time-dependent model exactly. We introduce a general scheme to disentangle the complex low-frequency Floquet spectrum to elucidate the relevant Floquet bands. As a prototypical example, we consider bilayer graphene. We find that light in the low-frequency regime can induce a band gap in the quasienergy spectrum in the vicinity of the K points even if it is linearly polarized, in contrast with the expectations within the Born-Oppenheimer approximation and the high-frequency regime. Finally, we analyze the diabaticity of the driven electron and driven phonon processes and find contrasting effects on the autocorrelation functions at the same driving frequency: Driven phonons preserve the character of the initial state while driven electrons exhibit strong deviations within a few drive cycles. The procedure outlined here can be applied to other materials to describe the combined effects of low-frequency light on phonons and electrons.
Learning crystal field parameters using convolutional neural networks
Noah F. Berthusen, Yuriy Sizyuk, Mathias S. Scheurer, Peter P. Orth, SciPost Phys, 11, 011 (2021)
We present a deep machine learning algorithm to extract crystal field (CF) Stevens parameters from thermodynamic data of rare-earth magnetic materials. The algorithm employs a two-dimensional convolutional neural network (CNN) that is trained on magnetization, magnetic susceptibility and specific heat data that is calculated theoretically within the single-ion approximation and further processed using a standard wavelet transformation. We apply the method to crystal fields of cubic, hexagonal and tetragonal symmetry and for both integer and half-integer total angular momentum values J of the ground state multiplet. We evaluate its performance on both theoretically generated synthetic and previously published experimental data on PrAgSb2 and PrMg2Cu9, and find that it can reliably and accurately extract the CF parameters for all site symmetries and values of J considered. This demonstrates that CNNs provide an unbiased approach to extracting CF parameters that avoids tedious multi-parameter fitting procedures.
Low-frequency and Moiré–Floquet engineering: a review
Martin Rodriguez-Vega, Michael Vogl, Gregory A. Fiete, Annals of Physics, 168434 (2021)
We review recent work on low-frequency Floquet engineering and its application to quantum materials driven by light, focusing on van der Waals systems hosting Moiré superlattices. These non-equilibrium systems combine the twist-angle sensitivity of the band structure with the flexibility of light drives. The frequency, amplitude, and polarization of light can be tuned in experimental setups, leading to platforms with on-demand properties. First, we review recent theoretical developments to derive effective Floquet Hamiltonians, emphasizing the low-frequency regime. We then review applications of some of these theories to study twisted graphene and transition metal dichalcogenide systems irradiated by light in free space and inside a waveguide. We study the changes induced in the quasienergies and steady-states, which can lead to topological transitions. Next, we consider van der Waals magnetic materials driven by low-frequency light pulses in resonance with the phonons. We discuss the phonon dynamics induced by the light and the resulting magnetic transitions from a Floquet perspective. We finish by outlining new directions for Moiré–Floquet engineering in the low-frequency regime and their relevance for technological applications.
Identification of strongly interacting organic semimetals
R. Matthias Geilhufe, Bart Olsthoorn, Phys. Rev. B 102, 205134 (2020)
Dirac- and Weyl point- and line-node semimetals are characterized by a zero band gap with simultaneously vanishing density of states. Given a sufficient interaction strength, such materials can undergo an interaction instability, e.g., into an excitonic insulator phase. Due to generically flat bands, organic crystals represent a promising materials class in this regard. We combine machine learning, density functional theory, and effective models to identify specific example materials. Without taking into account the effect of many-body interactions, we found the organic charge transfer salts (EDT-TTF-I2)2(DDQ)⋅(CH3CN) and TSeF-TCNQ and a bis-1,2,3-dithiazolyl radical conductor to exhibit a semimetallic phase in our ab initio calculations. Adding the effect of strong particle-hole interactions for (EDT-TTF-I2)2(DDQ)⋅(CH3CN) and TSeF-TCNQ opens an excitonic gap in the order of 60 meV and 100 meV, which is in good agreement with previous experiments on these materials.

Multi hole bands and quasi 2-dimensionality in Cr2Ge2Te6 studied by angle-resolved photoemission spectroscopy
In the present work, we investigate the electronic structure of the two-dimensional (2D) ferromagnet Cr2Ge2Te6 by photoemission spectroscopy and ab initio calculations. Our results demonstrate the presence of multiple hole-type bands in the vicinity of the Fermi level indicating that the material can support high electrical conductivity by manipulating the chemical potential. Also, our photon energy dependent angle resolved photoemission experiment revealed that several of the hole bands exhibit weak dispersion with varied incident photon energy providing experimental signature for its two dimensionality. These findings can pave the way for further studies towards the application of Cr2Ge2Te6 in electronic devices.
Robustness of topological corner modes in photonic crystals
We analyze the robustness of corner modes in topological photonic crystals, taking a C6-symmetric breathing honeycomb photonic crystal as an example. First, we employ topological quantum chemistry and Wilson loop calculations to demonstrate that the topological properties of the bulk crystal stem from an obstructed atomic limit phase. We then characterize the topological corner modes emerging within the gapped edge modes employing a semi-analytical model, determining the appropriate real space topological invariants. For the first time, we provide a detailed account of the effect of long-range interactions on the topological modes in photonic crystals, and we quantify their robustness to perturbations. We conclude that, while photonic long-range interactions inevitably break chiral symmetry, the corner modes are protected by lattice symmetries.
Group theory study of the vibrational modes and magnetic order in the topological antiferromagnet MnBi2Te4
Martin Rodriguez-Vega, A. Leonardo, and Gregory A. Fiete, Phys. Rev. B, 102, 104102 (2020)
We employ group theory to study the properties of the lattice vibrations and magnetic order in the antiferromagnetic topological insulator MnBi2Te4, both in bulk and few-layer form. In the paramagnetic phase, we obtain the degeneracies, the selection rules, and real-space displacements for the lattice vibrational modes for different stacking configurations. We discuss how magnetism influences these results. As a representative example, we consider a double septuple layer system and obtain the form of the magnetic order allowed by the symmetries of the crystal. We derive the allowed coupling terms that describe the paramagnetic to antiferromagnetic transition. Finally, we discuss the implications of our results for Raman scattering and other optical measurements. Our work sets the stage for a deeper understanding of the interplay of lattice modes, band topology, and magnetic order in MnBi2Te4 and other symmetry-related materials.
Superconductivity induced by fluctuations of momentum-based multipoles
Shuntaro Sumita, Youichi Yanase, Phys. Rev. Research, 2, 033225 (2020)
Recent studies of unconventional superconductivity have focused on charge or spin fluctuation, instead of electron-phonon coupling, as an origin of attractive interaction between electrons. On the other hand, a multipole order, which represents electrons’ degrees of freedom in strongly correlated and spin-orbit-coupled systems, has recently been attracting much attention. Stimulated by this background, we investigate multipole-fluctuation-mediated superconductivity, which proposes a new pairing mechanism of unconventional superconductivity. Indeed, previous works have shown spin-triplet superconductivity induced by fluctuations of odd-parity electric multipole orders in isotropic systems. In this study, we establish a general formulation of the multipole-fluctuation-mediated superconductivity for all multipole symmetries, in both isotropic and crystalline systems. As a result, we reveal various anisotropic pairings induced by odd-parity and/or higher-order multipole fluctuations, which are beyond the ordinary charge or spin fluctuations. Topological superconductivity due to the mechanism is also discussed. Based on the obtained results, we discuss unconventional superconductivity in doped SrTiO3, PrTi2Al20, Li2(Pd,Pt)3B, and magnetic multipole metals.
Phonon-mediated dimensional crossover in bilayer CrI3
In bilayer CrI3, experimental and theoretical studies suggest that the magnetic order is closely related to the layer staking configuration. In this work, we study the effect of dynamical lattice distortions, induced by nonlinear phonon coupling, in the magnetic order of the bilayer system. We use density functional theory to determine the phonon properties and group theory to obtain the allowed phonon-phonon interactions. We find that the bilayer structure possesses low-frequency Raman modes that can be nonlinearly activated upon the coherent photoexcitation of a suitable infrared phonon mode. This transient lattice modification in turn inverts the sign of the interlayer spin interaction for parameters accessible in experiments, indicating a low-frequency light-induced antiferromagnet-to-ferromagnet transition.
Magnetic and Electronic Properties of Complex Oxides from First‐Principles
The theoretical treatment of complex oxide structures requires a combination of efficient methods to calculate structural, electronic, and magnetic properties, due to special challenges such as strong correlations and disorder. In terms of a multi‐code approach, we combine various complementary first‐principles methods based on density functional theory to exploit their specific strengths. Pseudopotential methods, known for giving reliable forces and total energies, are used for structural optimization. The optimized structure serves as input for the Green’s function and linear muffin‐tin orbital methods. Those methods are powerful for the calculation of magnetic ground states and spectroscopic properties. Within the multi‐code approach, disorder is investigated by means of the coherent potential approximation within a Green’s function method or by construction of special quasirandom structures in the framework of the pseudopotential methods. Magnetic ground states and phase transitions are studied using an effective Heisenberg model treated in terms of a Monte Carlo method, where the magnetic exchange parameters are calculated from first‐principles. We demonstrate the performance of the multi‐code approach with different examples, including defect formation, strained films and surface properties.

Dirac materials for sub-MeV dark matter detection: New targets and improved formalism
Because of their tiny band gaps Dirac materials promise to improve the sensitivity for dark matter particles in the sub-MeV mass range by many orders of magnitude. We study several candidate materials and calculate the expected rates for dark matter scattering via light and heavy dark photons as well as for dark photon absorption. A particular emphasis is placed on how to distinguish a dark matter signal from background by searching for the characteristic daily modulation of the signal, which arises from the directional sensitivity of anisotropic materials in combination with the rotation of Earth. We revisit and improve previous calculations and propose two new candidate Dirac materials: bis(naphthoquinone)-tetrathiafulvalene (BNQ-TTF) and Yb3PbO. We perform detailed calculations of the band structures of these materials and of ZrTe5 based on density functional theory and determine the band gap, the Fermi velocities, and the dielectric tensor. We show that in both ZrTe5 and BNQ-TTF the amplitude of the daily modulation can be larger than 10% of the total rate, allowing us to probe the preferred regions of parameter space even in the presence of sizable backgrounds. BNQ-TTF is found to be particularly sensitive to small dark matter masses (below 100 keV for scattering and below 50 meV for absorption), while Yb3PbO performs best for heavier particles.
Engineering fragile topology in photonic crystals: Topological quantum chemistry of light
In recent years, there have been rapid advances in the parallel fields of electronic and photonic topological crystals. Topological photonic crystals in particular show promise for coherent transport of light and quantum information at macroscopic scales. In this work, we apply for the first time the recently developed theory of “topological quantum chemistry” to the study of band structures in photonic crystals. This method allows us to design and diagnose topological photonic band structures using only group theory and linear algebra. As an example, we focus on a family of crystals formed by elliptical rods in a triangular lattice. We show that the symmetry of Bloch states in the Brillouin zone can determine the position of the localized photonic wave packets describing groups of bands. By modifying the crystal structure and inverting bands, we show how the centers of these wave packets can be moved between different positions in the unit cell. Finally, we show that for shapes of dielectric rods, there exist isolated topological bands which do not admit a well-localized description, representing the first physical instance of “fragile” topology in a truly noninteracting system. Our work demonstrates how photonic crystals are the natural platform for the future experimental investigation of fragile topological bands.
Hund nodal line semimetals: The case of a twisted magnetic phase in the double-exchange model
R. M. Geilhufe, F. Guinea, and V. Juričić, Phys. Rev. B, 99, 020404(R) (2019)
We propose a class of topological metals, which we dub Hund nodal line semimetals, arising from the strong Coulomb interaction encoded in the Hund’s coupling between itinerant electrons and localized spins. We here consider a particular twisted spin configuration, which is realized in the double-exchange model which describes the manganite oxides. The resulting effective tetragonal lattice of electrons with hoppings tied to the local spin features an antiunitary nonsymmorphic symmetry that, in turn, together with another nonsymmorphic but unitary glide-mirror symmetry, protects crossings of a double pair of bands along a high-symmetry line on the Brillouin zone boundary. We also discuss the stability of Hund nodal line semimetals with respect to symmetry breaking arising from various perturbations of the twisted phase. Our results motivate further studies of other realizations of this state of matter, for instance, in different spin backgrounds, properties of its drumhead surface states, as well as its stability to disorder and interactions among the itinerant electrons.

Symmetry analysis of odd- and even-frequency superconducting gap symmetries for time-reversal symmetric interactions
R. M. Geilhufe and A. V. Balatsky, Phys. Rev. B, 97, 024507 (2018)
Odd-frequency superconductivity describes a class of superconducting states where the superconducting gap is an odd function in relative time and Matsubara frequency. We present a group theoretical analysis based on the linearized gap equation in terms of Shubnikov groups of the second kind. By discussing systems with spin-orbit coupling and an interaction kernel which is symmetric under the reversal of relative time, we show that both even- and odd-frequency gaps are allowed to occur. Specific examples are discussed for the square lattice, the octahedral lattice, and the tetragonal lattice. For irreducible representations that are even under the reversal of relative time the common combinations of s- and d-wave spin singlet and p-wave spin triplet gaps are revealed, irreducible representations that are odd under reversal of relative time give rise to s- and d-wave spin triplet and p-wave spin singlet gaps. Furthermore, we discuss the construction of a generalized Ginzburg-Landau theory in terms of the associated irreducible representations. The result complements the established classification of superconducting states of matter.

Three-dimensional organic Dirac-line materials due to nonsymmorphic symmetry: A data mining approach
R. M. Geilhufe, A. Bouhon, S. S. Borysov, and A. V. Balatsky, Phys. Rev. B., 95, 041103(R), 2017
A data mining study of electronic Kohn-Sham band structures was performed to identify Dirac materials within the Organic Materials Database. Out of that, the three-dimensional organic crystal 5,6-bis(trifluoromethyl)-2-methoxy-1H-1,3-diazepine was found to host different Dirac-line nodes within the band structure. From a group theoretical analysis, it is possible to distinguish between Dirac-line nodes occurring due to twofold degenerate energy levels protected by the monoclinic crystalline symmetry and twofold degenerate accidental crossings protected by the topology of the electronic band structure. The obtained results can be generalized to all materials having the space group P21/c (No. 14) by introducing three distinct topological classes.

