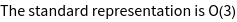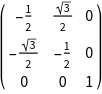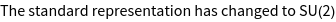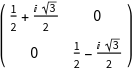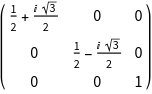GROUP THEORY TUTORIAL

Standard Representations – O(3), SU(2), SU(2)xS

GTPack allows for a symbolic manipulation of symmetry elements. However, internally all symmetry elements are represented by matrices. The corresponding matrix of a symmetry element can be obtained using GTGetMatrix. Depending on the application it might be necessary to switch between the representation used for the symmetry elements as will be shown in this Tutorial.

GTWhichRepresentationgives the currently used standard representation.
GTChangeRepresentationchanges the currently used standard representation.
GTGetMatrixgives a matrix corresponding to a symmetry element.

XXXX.

As a standard, GTPack represents all symmetry elements using 3D rotation matrices, i.e., matrices of the group O(3). The current standard representation can be checked using GTWhichRepresentation.
In[1]:=
Click for copyable input
In[2]:=
Click for copyable input
Out[2]=
In[3]:=
Click for copyable input
Out[3]//MatrixForm=
In[4]:=
Click for copyable input
Out[4]=
For studying spin - 1/2 systems, it is necessary to work with double groups. In such cases, it is useful to represent symmetry elements in terms of SU (2) matrices. The current standard representation can be changed using GTChangeRepresentation.
In[5]:=
Click for copyable input
In[6]:=
Click for copyable input
Out[6]//MatrixForm=
In[7]:=
Click for copyable input
Out[7]=
As can be seen, the consecutive application of two two-fold rotations about the same axis, i.e., a rotation by 360 ° degrees does not give the identity element, but the corresponding double group element denoted by an overbar. A spinor is an axial vector and spatial inversion does not affect a spinor basis function. As a result, the inversion operation is a 2*2 identity matrix if SU (2) matrices are considered. To properly represent improper symmetry elements, GTPack offers the product group representation SU (2) xS, with S = {1, -1}. This representation is required to install double groups with inversion symmetry.
In[8]:=
Click for copyable input
In[9]:=
Click for copyable input
Out[9]//MatrixForm=
In[10]:=
Click for copyable input
Out[10]//MatrixForm=
In the SU(2)xS representation every symmetry element is represented by a 3*3 matrix, where the upper left 2*2 block is an SU (2) matrix and the 3,3-element is either 1 or - 1, depending if the element is a proper or an improper rotation.