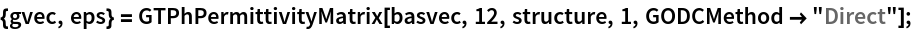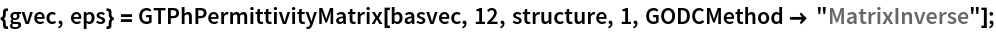GROUP THEORY SYMBOL

GODCMethod

GODCMethod
is an option to decide in wich way the Fourier transform of is calculated.

DetailsDetails

  • The Fourier transform of is needed to set up the master equation can be found in two ways. First, it can be calculated directly by Fourier transform of , the so called direct method. In the second method, the method of matrix inverse (Ho’s method) the Fourier transform of is calculated first. The corresponding matrix is inverted afterwards.
  • Typical values for GODCMethod are:
  • "Direct"Fourier transform of .
    "MatrixInverse"Fourier transform of followed by matrix inversion.
  • This option is used by: GTPhBandsObjects bullet GTPhPermittivityMatrix

ExamplesExamplesopen allclose all

Basic Examples  (1)Basic Examples  (1)

First load the package:

In[1]:=
Click for copyable input

As an example dielectric rods in a square lattice in air are considered. The structure is defined:

In[2]:=
Click for copyable input

The path in the Brillouin zone is fixed.

In[3]:=
Click for copyable input

The Fourier transform of 1/ϵ(r) is calculated

In[4]:=
Click for copyable input

The eigenvalue problem is constructed for the TM polarization. The photonic band is calculated and plotted.

In[5]:=
Click for copyable input
Out[5]=

The Fourier transform of ϵ(r) is calculated and the corresponding matrix is inverted afterwards.

In[6]:=
Click for copyable input

Calculation of the photonic band structure with this method.

In[7]:=
Click for copyable input
Out[7]=
In[8]:=
Click for copyable input
Out[8]=

Small differences occur due to the limited set of plane waves used in the calculation.

Top