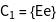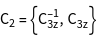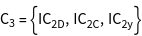GROUP THEORY SYMBOL
GTCharacterTable
GTCharacterTable[group]
gives the character table of a group.
DetailsDetails
- The trace of the representation matrix
![TemplateBox[{T}, Gamma] TemplateBox[{T}, Gamma]](Files/GTCharacterTable/4.png) of an element
of an element 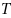 of a group
of a group 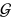 is called character
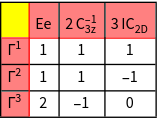
is called character 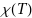 . The character systems of the irreducible representations of a finite group are conventionally displayed in the form of a "character table".
. The character systems of the irreducible representations of a finite group are conventionally displayed in the form of a "character table". - All elements in the same class have the same character.
- The number of inequivalent irreducible representations is equal to the number of classes of a finite group
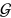 .
. - For a finite group a necessary and sufficient condition for two representations to be equivalent is provided by the equality of their character systems.
- If a group
 is finite, the sum of the squares of the dimensions of the inequivalent irreducible representations is equal to the order of
is finite, the sum of the squares of the dimensions of the inequivalent irreducible representations is equal to the order of  .
. - The output of GTCharacterTable is a list of all classes, a list of the character system and a list of the names of the irreducible representations.
- Attention: The names of the irreducible representations are generated automatically and may differ from tables in the literature!
- The following options can be given:
-
GOIrepNotation "Bethe" Notation for irreducible representations GOVerbose True Controls the output of information GOFast GOFastValue Skips the input vlidation GOReality False Provides information about the reality of the irreducible representations GOMethod "NumericalApproximant" Method for internal eigenvalue solution - See: W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica, chapter 5.8