GTPhDCPixel
GTPhDCPixel[reciprocal lattice vector,pixelmap,basis vectors]
calculates the Fourier transform 
of the inverse permittivity for a reciprocal lattice vector, if 
Details
- The pixelmap defines the distribution of the permittivity in the unit cell. All pixels have the same geometrical form. Hence,
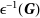of the whole cell is constructed from the Fourier transforms of the individual pixels. - basis vectors defines the geometry of the pixel:
- basis vectors = {a,b,ϕ}
- Therefore a squared unit cell, a rectular unit cell or an oblique-angled unit cell is possible.
- The following option can be given:
-
GOVerbose False Controls the output of additional information. - See: W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica, chapter 10.4
Examplesopen all
Basic Examples (1)
| In[1]:= |
| In[2]:= |
A pixel map of the permittivity distribution is defined.
| In[3]:= |
Note, to define pixel maps you can often use effectively RegionMember
The structure is plotted. There is no modification defined. The unit cell is a square.
The basis vectors in the square lattice are given by:
| In[5]:= |
ϵ-1(G)for G={1,0,0} follows to be:
Comparison with analytical result for the prismatic rod
The simple geometric distribution of 
in the unit cell in the example above allows to find an analytical result for the Fourier transform. This is also implemented in GTPack.
The side length of the rod is 2/3 of the lattice constant. 
is assumed for the structure.
| In[7]:= |
The same distribution of the permittivity is defined for the analytical calculation.
The analytical formula leeds to the same result like the definition by means of the pixel map.
