GROUP THEORY SYMBOL
GTGroupQ
Details
- A set
of elements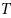 
is called group if the four group axioms are satisfied: - a) Closure: There exists an operation called multiplication which associates with every pair of elements
and 
of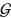 
to another Element 
of 
. - b) Associativity: For any three elements
, 
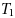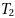and 
of 
the "associative law" is valid. - c) Identity element: There exists an Element
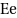which is contained in 
such that for every element 
. - d) Inverse element: For each element
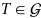there exists an inverse Element 
which is also contained in 
such that: 
. - The input can be of type symbol, matrix, quaternion or Euler angles (compare GTEulerAnglesQ, GTQuaternionQ and GTSymbolQ).
-
GOMethod "Numeric" Specifies the method to determine if a given list of elements is a group. - See: W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica, chapter 3.1.
