GROUP THEORY SYMBOL

GTTbHamiltonianElement

GTTbHamiltonianElement[l1,m1,l2,m2,shell,shell vectors]
constructs the k-dependent contribution of shell characterized by the shell vectors to the tight-binding matrix element between functions of symmetry and .

DetailsDetails

  • The tables in the seminal paper of Slater and Koster and a series of other papers in the field contain the k-dependent matrix elements of a tight-binding Hamiltonian including usually (*), and 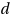functions.
  • The tables are given for certain crystal structures. GTTbHamiltonianElement generates the analytical expressions automatically and therefore avoids mistakes. k-vectors are represented in units of 2π/a. The components of the k-vector are , , .
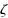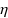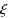  • The following option can be given:
  • GOTbBasis0Supresses superscripts with element names
  • See: J. C. Slater, G. F. Koster,Simplified LCAO method for the periodic potential problem, Phys. Ref. 94, 1498-1524 (1954)
  • W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica, chapter 9.4.

ExamplesExamplesopen allclose all

Basic Examples  (1)Basic Examples  (1)

First load the package.

In[1]:=
Click for copyable input

We assume a cubic lattice. The vectors of the nearest neighbor shell are:

In[2]:=
Click for copyable input

The Hamilton matrix element between to s function is given by

In[3]:=
Click for copyable input
Out[3]=

This is exactly the form given by Slater and Koster., , are the components of the k-vector in units 2π/a.

Other Examples:

In[4]:=
Click for copyable input
Out[4]=
Out[4]=
Out[4]=

In some considerations of semiconductors an excited orbital * is included in the basis. This can be simulated using .

In[5]:=
Click for copyable input
Out[5]=

Options  (1)Options  (1)

Top