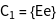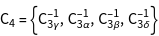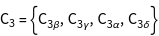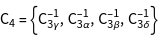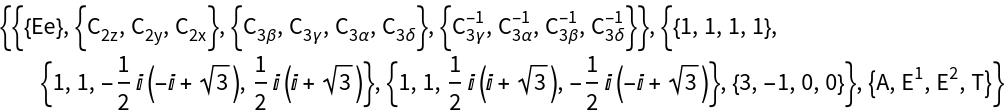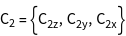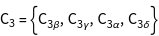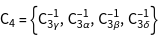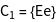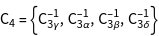GROUP THEORY TUTORIAL
Installation of Point Groups and Character Tables
The example shows the installation of point groups using GTInstallGroup and the calculation of charcater tables using GTCharacterTable.
| GTInstallGroup | installs a point or space group |
| GTCharacterTable | gives the character table of a group |
| GOIrepNotation | is an option to specify the used notation for irreducible representation |
| GOReality | is an option to decide whether additional information about the reality of irreducible representations are printed within the character table. |
For our example we use the tetrahedral point group T, containing 12 elements. In general, point groups, space, groups, and double groups can be installed using the module GTInstallGroup. For our example, the relevant code would be:
| In[1]:= |
Point groups can be denoted in various ways. The name T is the name of the above installed group in the Schönflies notation. Similarly, the same group can be installed using the Hermann-Mauguin notation, where the corresponding name is given by 23. To avoid confusion of such point group names with space group numbers, the Hermann-Mauguin notation needs to be embedded in | … | as shown in the following.
The character table of the group is installed using GTCharacterTable. The point group T contains 4 classes and therefore 4 irreducible representations.
Various notations for irreducible representations of point groups exist.GTPack supports the Mulliken notation [J.Chem.Phys.23, 1997 (1955)] and the notation proposed by Bouckaert, Smoluchowski, and Wigner [Phys.Rev.50, 58 (1936)]. The notation can be chosen by specifying the option GOIrepNotation. The Mulliken notation is obtained as follows :
While irreducible representations are complex in general, similarity transformations into a set of real matrices exist in various cases. As such, irreducible representations can be classified with respect to their "reality" as "potentially real", "essentially complex", or "pseudo-real". This behavior is important when time-reversal symmetry is taken into account. By specifying the option GOReality this additional property of irreducible representations is determined :