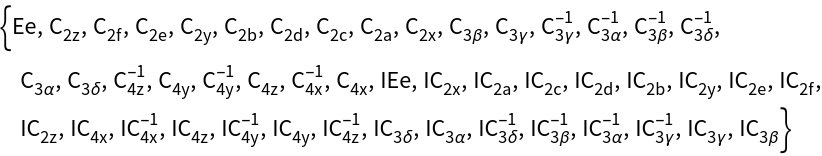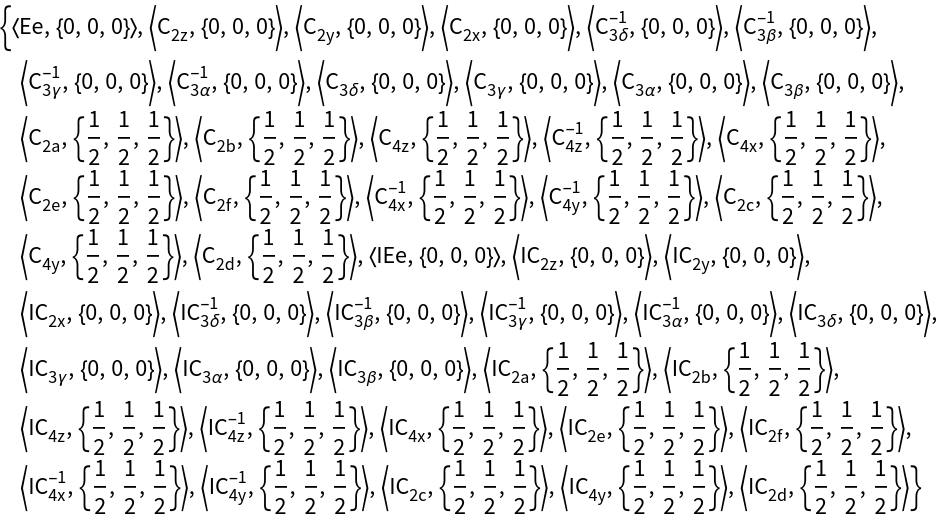GROUP THEORY SYMBOL
- Tutorials
-
See Also
- GTChangeRepresentation
- GTCharacters
- GTCrystalSystem
- GTExtraRepresentations
- GTGroupFromGenerators
- GTGroupHierarchy
- GTGroupNotation
- GTGroupOfK
- GTGroupOrder
- GTIcosahedronAxes
- GTInstallAxis
- GTInstallColorGroup
- GTIrepMatrixView
- GTPointGroups
- GTRegularRepresentation
- GTReinstallAxes
- GTReorderCharacterTable
- GTShowSymmetryElements
- GTSymmetryElementQ
- GTTableToGroup
- GTWhichRepresentation
- Related Guides
GTInstallGroup
GTInstallGroup[group]
gives a faithful representation of a crystallographic group.
DetailsDetails
- Within the GTPack the crystallographic point groups are implemented. According to GORepresentation, GTInstallGroup gives O(3) matrices for ordinary crystallographic point groups, SU(2) matrices for double groups without inversion, matrices of the outer direct product SU(2)x{1,-1} for double with inversion ("SU(2)xS"), as well as O(2) matrices for 2-dimensional point groups.
- group can be a string or a symbol in Schönflies notation or a symbol in bracketing bars in Hermann–Mauguin notation.
- Use GTGroupHierarchy to get an overview over all installed crystallographic point groups.
- The palette contains all point group symbols and can be used to install the corresponding groups.
- The following options can be given:
-
GORepresentation "O(3)" Defines the used standard representation GOVerbose True Controls the output of additional information - See: W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica, chapter 3.1, 5.1.
See AlsoSee Also
GTChangeRepresentation ![]() GTCharacters
GTCharacters ![]() GTCrystalSystem
GTCrystalSystem ![]() GTExtraRepresentations
GTExtraRepresentations ![]() GTGroupFromGenerators
GTGroupFromGenerators ![]() GTGroupHierarchy
GTGroupHierarchy ![]() GTGroupNotation
GTGroupNotation ![]() GTGroupOfK
GTGroupOfK ![]() GTGroupOrder
GTGroupOrder ![]() GTIcosahedronAxes
GTIcosahedronAxes ![]() GTInstallAxis
GTInstallAxis ![]() GTInstallColorGroup
GTInstallColorGroup ![]() GTIrepMatrixView
GTIrepMatrixView ![]() GTPointGroups
GTPointGroups ![]() GTRegularRepresentation
GTRegularRepresentation ![]() GTReinstallAxes
GTReinstallAxes ![]() GTReorderCharacterTable
GTReorderCharacterTable ![]() GTShowSymmetryElements
GTShowSymmetryElements ![]() GTSymmetryElementQ
GTSymmetryElementQ ![]() GTTableToGroup
GTTableToGroup ![]() GTWhichRepresentation
GTWhichRepresentation