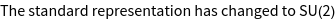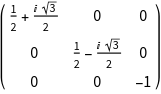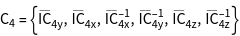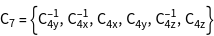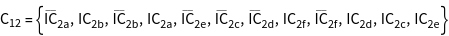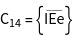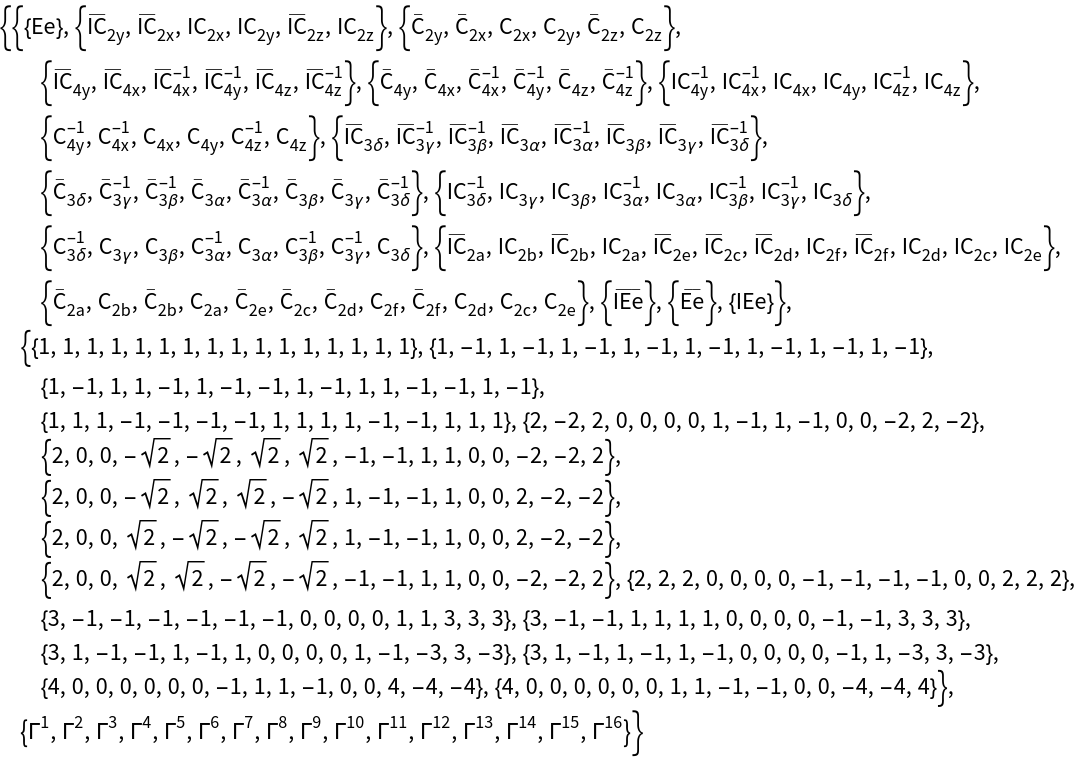GROUP THEORY TUTORIAL
Installation of Double Groups
For the implementation of double groups we follow the definition of Damhus [Match 16:21–82 (1984)].
| GTInstallGroup | installs a point or space group |
| GORepresentation | specifies the used standard representation |
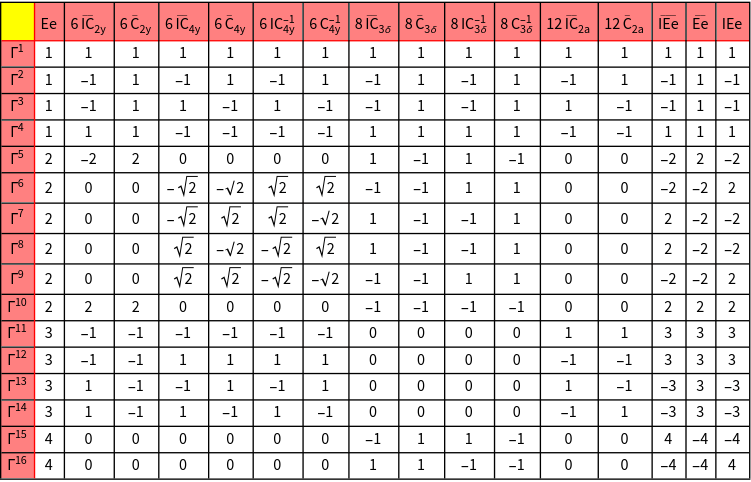
| GTCharacterTable | gives the character table of a point group |
We start with a point group which does not contain inversion symmetry, e.g., the point group O. For ordinary point groups the symmetry elements can be represented using 3D rotation matrices, i.e. matrices of the group O(3). However, for double groups without inversion symmetry, the symmetry elements are represented using SU(2) matrices. Double groups without inversion symmetry are installed using GTInstallGroup and specifying the option GORepresentation->”SU(2)”.
| In[1]:= |
While O contains 24 elements, the double group of O contains 48 elements, where double group elements are denoted with an overbar. By specifying the option GORepresentation, the standard representation used by GTPack is changed and elements are internally represented by SU (2) matrices.
As a result, rotations by 720° represent the identity, whereas rotations by 360° constitute a factor - 1 to a spinor basis function.
A spinor is an axial vector and spatial inversion does not affect a spinor basis function. As a result, the inversion operation is a 2*2 identity matrix if SU (2) matrices are considered. To properly represent a point group with inversion symmetry, symmetry elements are therefore represented by a product group SU(2)xS, with S = {1, -1}. Using GTInstallGroup and specifying GORepresentation a point group containing inversion symmetry, e.g., Oh is installed as follows.
In the SU(2)xS representation every symmetry element is represented by a 3x3 matrix, where the upper left 2x2 block is an SU(2) matrix and the 3,3-element is either 1 or - 1, depending if the element is a proper or an improper rotation.
Character tables, etc.of double groups are obtained in a similar manner as for ordinary groups using GTCharacterTable.