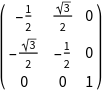GROUP THEORY TUTORIAL
Handling of symmetry elements: multiplication, symbols, matrices, etc.
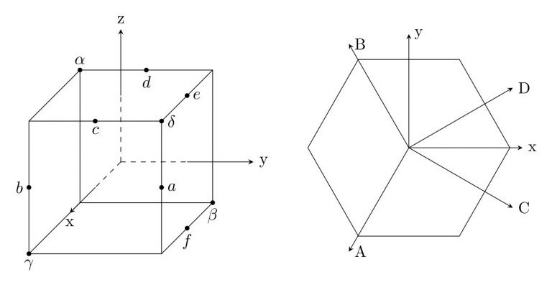
GTPack allows for a symbolic handling of symmetry elements, where e.g. C3z denotes a threefold rotation about the z-axis (120°) or C4x a fourfold rotation about the x-axis (90°). All preinstalled symmetry axes are shown below:
| GTgmat | performs a multiplication of two symmetry elements |
| GTGetMatrix | gives a matrix corresponding to a symmetry element. |
| GTGetSymbol | gives the symbol of a symmetry element |
| GTGetRotationMatrix | gives the 3D rotation matrix of a symmetry element |
| GTGetSU2Matrix | gives the SU(2) matrix of a symmetry element |
| GTGetEulerAngles | gives the Euler angles and the determinant of the 3D rotation matrix of a symmetry element |
| GTGetQuaternion | gives the quaternion of a symmetry element |
| GTInstallAxis | installs symmetry elements with respect to a given rotation axis |
Such symmetry elements can be multiplied using GTgmat or simply in symbolic form combining the elements with a ∘.
| In[1]:= |
Internally, matrices are used to handle symmetry elements.The corresponding matrix can be obtained using GTGetMatrix.
GTGetMatrix depends on the current standard representation. However, in some cases it might be necessary to obtain the 3D rotation matrix or the corresponding SU(2) matrix. The relevant commands are GTGetRotationMatrix and GTGetSU2Matrix.
The corresponding symbol of a matrix can be obtained using GTGetSymbol.
Similarly, symmetry elements can be represented as quaternions or in terms of three Euler Angles and the determinant of the rotation matrix.
Besides the preinstalled symmetry axes, which can be checked from the variable axeslist, new symmetry axes can be installed using GTInstallAxis.