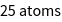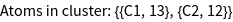GROUP THEORY TUTORIAL
Tight-binding electronic structure of graphene
We illustrate the generation of effective tight-binding Hamiltonians in the two-center Slater-Koster formalism for the 2-dimensional carbon allotrope graphene.
| GTCluster | constructs a spherical cluster crystal structure. |
| GTShells | performs a reordering of a cluster of atoms into shells |
| GTTBHamiltonian | constructs a k-dependent tight-binding Hamiltonian |
| GTHamiltonianPlot | plots the structure of a Hamiltonian |
| GTBZPath | generates a standard path in the Brillouin zone |
| GTBandStructure | calculates and plots the band structure for a given Hamiltonian |
| GTBands | calculates the lowest band energies for a given Hamiltonian |
Graphene crystallizes in a 2-dimensional honeycomb lattice with two atoms in the primitive unit cell. In GTPack, structures are specified as a list, where the list contains the name of the structure and a prototype, four different names for the space group (Pearson symbol, Strukturbericht designation, international notation, and space group number), the lattice, and the sites containing the atom name and the atom position. Note that the first five information are optional and not important for the generation of the tight-binding model. The structure itself can be plotted using GTPlotStructure2D. In our example we choose the lattice constant to be a = 1 a.u. and plot the structure within a radius of 5 a.u..
| In[1]:= |
| In[2]:= |
For the construction of the tight-binding model it is necessary to construct a real space cluster. This cluster is reordered into different shells corresponding to nearest neighbor, next nearest neighbor, next next nearest neighbor interactions, etc. The respective commands to do so are GTCluster and GTShells. Originating from each of the two carbon atoms in the unit cell we choose to construct a cluster of a radius of 3 a.u. about both atoms. Using the option GOTbLattice one can specify which interaction are to be taken into account. Here we choose a nearest neighbor tight-binding model, where only the first shell of the two nonequivalent carbon atoms is taken into account. We furthermore set the onsite interaction to zero. Using GOPosition we set the algorithm to work in relative coordinates.
Using the information for the corresponding shells as well as an orbital basis, a tight-binding Hamiltonian is constructed using GTTbHamiltonian. The orbital basis is specified as a list containing : i) the name of the site or type; ii) the number of atoms of this type; iii) a list of angular momenta to be taken into account. In our example we consider s–(l = 0) and p - orbitals (l = 1) only, so the angular momentum information is {0, 1}. To obtain a better overview of the non-zero matrix elements of the Hamiltonian, GTHamiltonianPlot is used.
As can be verified, all orbitals with in - plane components hybridize, i.e., s -, px -, and py - orbitals. However, the pz-orbitals do not hybridize with any of the other orbitals, leading to a 2x2 sub-matrix which is extracted from the full Hamiltonian in the following. Furthermore, we apply GTBZPath to obtain a standard path for the band structure calculation.
| In[7]:= |
The final band structure plot is obtained using the command GTBandStructure. We set the on-site energies to zero and choose a value of 1 (in arbitrary units) for the nearest neighbor hopping strength. GTBandStructure requires the Hamiltonian, the high-symmetry points of the Brillouin zone path, the number of mesh points used along each segment of the Brillouin zone path, as well as the number of bands to be plotted.
| In[9]:= |