In crystal field theory, I would like to know how to calculate the basis function of a sub group of O(3) in fucntion of the initial spherical harmonics basis.
For instance, in the Figure 7.2 example (d-state splitting in a crystal field), it is possible to express the basis of the B2g representation of the D4h symmetry, in function of the T2g representation of the Oh symmetry thanks to the GTClebschGordanTable. But how to do the same for Oh and O(3) so: how to express the basis functions of the T2g representation of the Oh symmetry in function of the basis (that are the spherical harmonics of J=2) of the D2 representation of O(3)?
I did not find an easy way even using GTAngularMomentumChars or GTWignerProjectionOperator ??
Hi Daniel,
GTPack has a function called “GTAngularMomentumRep” which gives the representation matrices of O(3) (or SU(2)) in the basis of spherical harmonics. I suggest using this function and setting up a character projection operator as explained in Sec. 5.4 of the book,
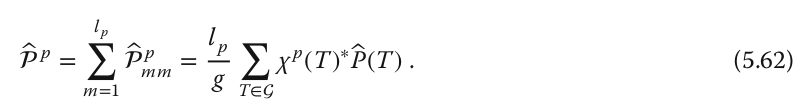
(l_p is the dimension of the irreducible representation, g the order of the group, chi(T) the characters). P(T) is a projection operator, which, for the basis of spherical harmonics, is given by

The function D^l_m’m(T) is the output of GTAngularMomentumRep.
I attach a complete example, which looks lengthy. However, the actual calculation is only a few lines.


Many thanks for the answer (and for the wonderful Pack!)