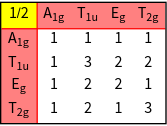
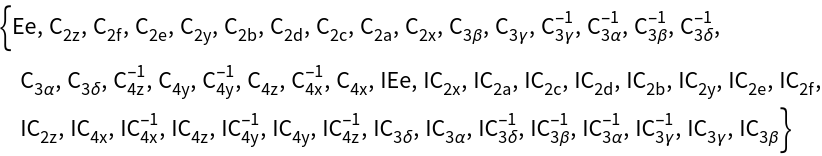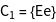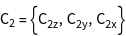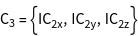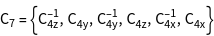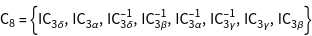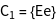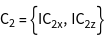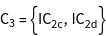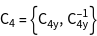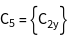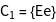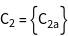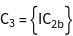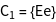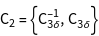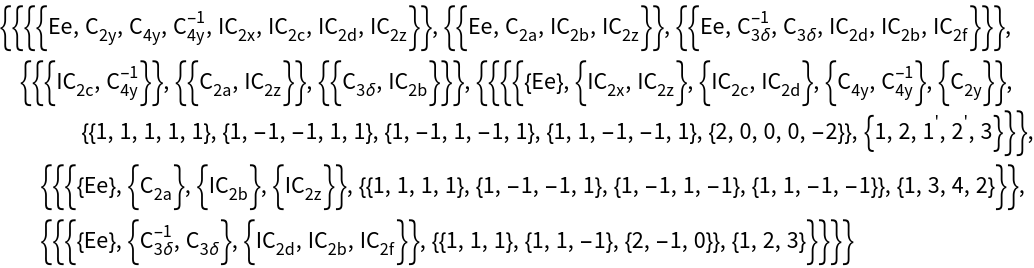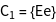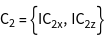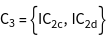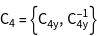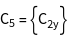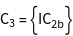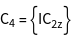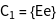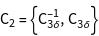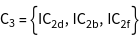GTTbNumberOfIntegrals
GTTbNumberOfIntegrals[character table, subgroup character tables,irreducible representations]
gives the number of independent Integrals in a three-center tight-binding Hamiltonian for a certain shell.
Details
- The point group of the crystal is
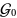. The crystal is considered as a series of shells of atoms of constant distance from a central atom. The shells 
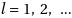are characterized by the shell vectors 
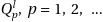. The groups 
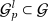contain the elements of 
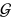that transform the shell vectors in the vectors 
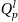. The information about the character tables of 
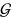and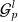 
is used to calculated the number of independent integrals in a three-center tight-binding Hamiltonian. - The following options can be given:
-
GONames {} Controls the names of irreducible representations GOVerbose False Controls the output of additional information - See: R.F. Egorv, B.I. Reser, V.P. Shirkovskii,Consistent Treatment of Symmetry in the Tight Binding Approximation, phys. stat. sol. 26, 391 (1968)
- W. Hergert, M. Geilhufe, Group Theory in Solid State Physics and Photonics. Problem Solving with Mathematica
Examplesopen all
Basic Examples (1)
| In[1]:= |
The point group 
is considered.
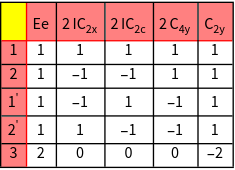
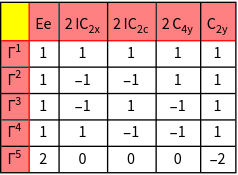
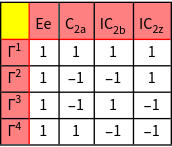
The character table of the group is calculated. The notation of Mulliken is used.
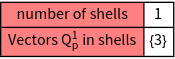
qv contains the vectors 
of shell 
which are the minimum set to recalculate all vectors of the coordination sphere by point group operations. In case of the simple cubic lattice it is one vector per coordination sphere.
| In[4]:= |
The groups 
of the vectors 
, i.e. all operations of the point group, leaving the vectors constant, are generated.
| In[6]:= |
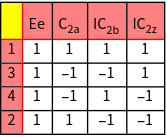
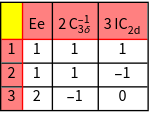
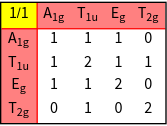
The character tables of the groups.
The number of independet integrals can be calculated now for each shell.
| In[8]:= |
